Definitionsbereich / Definitionsmenge

Was man unter dem Definitionsbereich versteht, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, was Definitionsbereich bzw. Definitionsmenge sind.
• Beispiele für das Ermitteln der Definitionsmenge.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zum Definitionsbereich.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Es ist hilfreich, wenn ihr bereits wisst, was ein Bruch ist, was eine Wurzel ist und was ein Logarithmus ist.

Definitionsbereich Erklärung

In der Mathematik beschäftigt man sich regelmäßig mit Funktionen. Manchmal darf man in diese Funktionen bestimmte Zahlen nicht einsetzen. Definition:

In Mathematik-Aufgaben wird meistens nach dem maximalen Definitionsbereich gefragt. Dies umfasst damit alle Zahlen, welche aus Sicht der Mathematik eingesetzt oder nicht eingesetzt werden dürfen. Zusätzlich kann der Ersteller der Aufgaben selbst noch Zahlen ausschließen.

Bei der Kurvendiskussion - so wie diese in der Oberstufe durchgeführt wird - interessiert man sich dafür, welche Zahlen man nicht einsetzen kann: Brüche dürfen im Nenner nicht Null werden, unter der Wurzel darf keine negative Zahl stehen und ein Logarithmus muss größer als Null sein. Wir merken uns:

Anzeige:

Definitionsbereich Beispiel

Sehen wir uns einige Beispiele zum Definitionsbereich (Definitionsmenge) an. In diesem Zusammenhang wird gezeigt, wie man den Definitionsbereich berechnet und wie die Schreibweise zum Angeben der Definitionsmenge aussieht.

Beispiel 1: Bruchgleichung Definitionsbereich

Starten wir mit dem Definitionsbereich für einen Bruch bzw. eine Bruchgleichung. Wir haben dabei 2x - 4 im Nenner. In der Mathematik gilt: Durch Null darf nicht geteilt werden. Der Nenner des Bruchs darf aus diesem Grund nicht Null werden. Wir setzen dazu den Nenner gleich Null und berechnen, bei welchem x dies passieren würde. Bei x = 2 wäre dies der Fall.

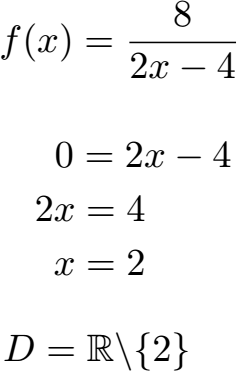
Wie lautet die Schreibweise für die Definitionsmenge? Dafür gibt es oft mehrere Möglichkeiten. In diesem Fall können wir dies zum Beispiel so schreiben, dass die Definitionsmenge D alle rationalen Zahlen (R) sind ohne die 2. Die rationalen Zahlen kürzt man dabei mit einem R mit zwei Strichen ab. Der Schrägstrich mit "\" steht für ein "ohne", in diesem Fall ohne die 2.

Beispiel 2: Wurzel Definitionsmenge

Für die Wurzel aus 3x + 6 soll die Definitionsmenge ausgerechnet werden. Wichtig dabei ist zu wissen, dass unter der Wurzel eine Zahl entstehen muss, die 0 oder größer sein muss.

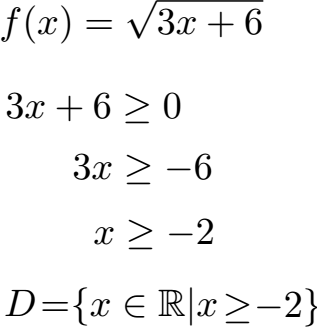
Zur Schreibweise der Definitionsmenge: Alle rationalen Zahlen sind erlaubt die größer oder gleich -2 sind.

Beispiel 3: Logarithmus Definitionsbereich

Im dritten Beispiel nehmen wir den natürlichen Logarithmus von 4x + 12. Dabei muss der Logarithmus von irgend etwas größer als Null sein. Um dies zu berechnen, muss 4x + 12 größer als Null sein. Dies ist der Fall wenn x > -3 ist.

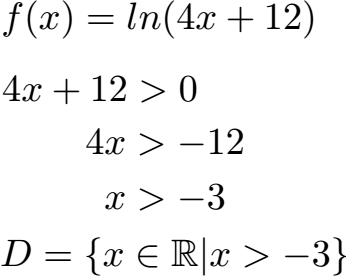
Von der Schreibweise her schreiben wir in die Definitionsmenge rein, dass wir alle rationalen Zahlen erlauben die größer als -3 sind.

Aufgaben / Übungen Definitionsemenge

Aufgabe 1:

Bevor wir rechnen erst einmal eine kurze Frage.

• Wie wird der Definitionsbereich noch genannt?

• Definitionsart
• Definitionsmenge
• Definitionsklammer
• Mengenzusammenfassung

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Definitionsbereich

Fragen mit Antworten zum Definitionsbereich