Monotoniesatz / Monotoniekriterien
Geschrieben von: Dennis RudolphMontag, 16. Dezember 2019 um 10:35 Uhr
Mit dem Monotoniesatz und den Kriterien für Monotonie befassen wir uns hier. Dies sehen wir uns an:
- Eine Erklärung, was Monotonie und Monotoniesatz sind.
- Beispiele für grafische und rechnerische Monotoniekriterien.
- Aufgaben / Übungen um das Thema selbst zu üben.
- Ein Video zu Extrempunkten.
- Ein Frage- und Antwortbereich zu diesem Thema.
Tipp: Um die Monotoniebedingungen zu verstehen und berechnen zu können, solltet ihr bereits Ableitungsregeln kennen.
Monotoniesatz Erklärung
Beginnen wir ganz kurz mit einer Definition:
Unter der Monotonie einer Funktion versteht man das Steigungsverhalten. Daraus ergibt sich eine bzw. mehrere Monotoniebedingungen einer Funktion. Mit dem Monotoniesatz gibt man die Bedingungen an wann eine Funktion (streng) monoton wächst oder (streng) monoton fällt.
Um dies zu verstehen werft einen Blick auf die nächste Grafik. Dort ist eine Funktion in vier Gebiete unterteilt und jeweils die Monotonie angegeben.
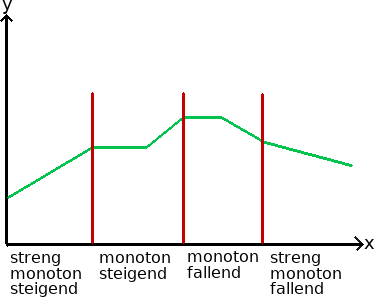
Die Monotoniekriterien bzw. der Monotoniesatz werden über die erste Ableitung angegeben:
- Streng monoton wachsend heißt der Verlauf der Funktion geht nur nach oben (nie seitlich und nie abwärts). Der Wert der Funktion steigt von links nach rechts an: f'(x) > 0.
- Monoton wachsend heißt die Funktion steigt in einem Bereich und in einem anderen Teilbereich verläuft sie seitlich (aber nie abwärts). Der Wert der Funktion steigt von links nach rechts an oder bleibt gleich: f'(x) ≥ 0
- Streng monoton fallend heißt die Funktion fällt nur (nie seitlich, nie nach oben). Der Wert der Funktion fällt von links nach rechts: f'(x) < 0.
- Monoton fallend heißt das in diesem Bereich die Funktion teils abwärts geht und teils seitlich läuft (aber nie steigt). Der Wert der Funktion fällt oder bleibt gleich: f'(x) ≤ 0.
Funktionen können je nach Bereich ein unterschiedliches Verhalten in der Monotonie aufweisen.
Anzeige:
Anzeigen:
Monotoniekriterien anwenden Beispiel
Im nächsten Beispiel sollen die Monotoniekriterien gezeigt werden.
Beispiel 1: Monotoniesätze anwenden
Wir haben die folgende Gleichung. Wie sieht das Verhalten der Monotonie aus?
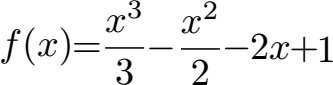
Lösung:
Die erste Möglichkeit besteht darin die Funktion zu zeichnen und sich die Monotonie anzusehen. Wirft man einen Blick auf die nächste Grafik sieht man, dass die Funktion zunächst steigt. Bei dem "Berg" links der x-Achse muss ein Hochpunkt liegen. Rechts der x-Achse gibt es ein "Tal" mit einem Tiefpunkt. Weiter rechts steigt die Funktion wieder.
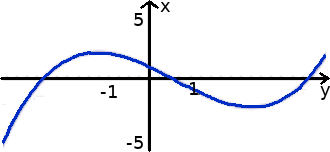
Wo die Extremstellen (Hochpunkt und Tiefpunkt) genau liegen sieht man der Funktion hier nur grob an. Exakt ablesen kann man dies so nicht. Außerdem soll jeder dies auch rechnen können.
Zunächst leiten wir die Funktion ein Mal ab und berechnen die Nullstellen. Diese liegen bei x = -1 und x = +2. Danach bilden wird die zweite Ableitung und setzen dort für x nun -1 und +2 ein. Bei x = -1 erhalten wir -3. Daher liegt hier ein Hochpunkt vor. Für x = 2 erhalten wir +3, daher liegt ein Tiefpunkt vor.
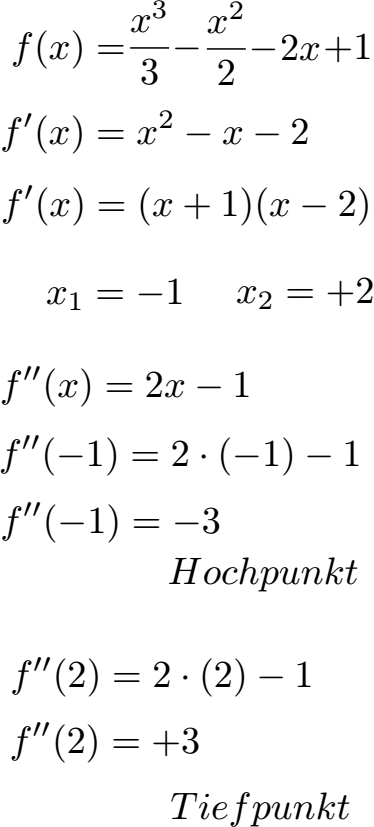
Was bedeutet dies nun?
- Ein Hochpunkt bedeutet, dass wir über einen "Berg" müssen.
- Erst hoch, dann runter.
- Also erst (streng) monoton steigend, danach (streng) monoton fallend.
- Ein Tiefpunkt bedeutet, dass wir durch ein "Tal" müssen.
- Erst runter, dann hoch.
- Also erst (streng) monoton fallend, danach (streng) monoton steigend.
Aufgaben / Übungen Monotonie
Anzeigen:Video Extrempunkte
Beispiele und Erklärungen
Teil von Monotoniekriterien bzw. den Monotoniesätzen ist das Berechnen der Extrempunkte. Aus diesem Grund sehen wir uns dies im nächsten Video an:
- Was sind Extrempunkte bzw. Extremstellen?
- Was ist ein Hochpunkt bzw. Hochstellen?
- Was ist ein Tiefpunkt bzw. Tiefstellen?
- Wie sehen solche Extrempunkte / Extremstellen aus?
- Wie berechne ich diese Punkte / Stellen?
- Ein Beispiel wird vorgerechnet und erläutert.
Nächstes Video »
Fragen mit Antworten zur Monotonie
In diesem Abschnitt sehen wir uns typische Fragen mit Antworten zur Monotonie an.
F: Wie geht man vor wenn man Extremstellen bestimmen möchte?
A: Um die Monotonie zu erkennen berechnet man Extremstellen. Hier eine kleine Anleitung dazu, wie man dies tut:
- Erste Ableitung bilden
- Wir setzen die erste Ableitung gleich Null und berechnen x.
- Zweite Ableitung bilden.
- In diese zweite Ableitung setzen wir die berechneten x-Werte der ersten Ableitung ein.
- Ist dies größer 0 liegt ein Tiefpunkt vor.
- Ist dies kleiner 0 liegt ein Hochpunkt vor.
F: Welche Ableitungsregeln und Ableitungsthemen sollte ich kennen?
A: Die folgenden Themen werden in der Schule zu Ableitungen behandelt.
- Differentialrechnung Übersicht
- Ableitung: Grundlagen und Definition
- Ableitung Tabelle / Ableitungstabelle
- Ableitungsregeln
- Kurvendiskussion
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
