Punktsymmetrie zu beliebigem Punkt

Mit der Punktsymmetrie zu einem beliebigem Punkt befassen wir uns hier. Dies sehen wir uns an:

• Eine Erklärung, wie man Punktsymmetrie zu einem Punkt erkennt.
• Beispiele wie man diese Art der Punktsymmetrie prüft.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zur Symmetrie von Funktionen.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Es ist hilfreich wenn ihr bereits wisst wie man die Punksymmetrie zum Ursprung erkennt. Diese ist deutlich einfacher zu bestimmen und sollte daher als Grundwissen bei euch vorhanden sein.

Erklärung Punktsymmetrie zu Punkt

In der Oberstufe bis hin um Abitur steht in Mathematik die Kurvendiskussion auf dem Lehrplan. Ein Teil der Kurvendiskussion ist die Untersuchung auf Punktsymmetrie. Dabei unterscheidet man zwei typische Untersuchungen:

• Punktsymmetrie zum Ursprung
• Punktsymmetrie zu einem bestimmten Punkt

Wichtig: Man kann noch weitere Dinge in der Symmetrie untersuchen. Aber diese beiden Punkte werden sehr oft betrachtet. Hier sehen wir uns die Punktsymmetrie zu einem beliebigem Punkt an.

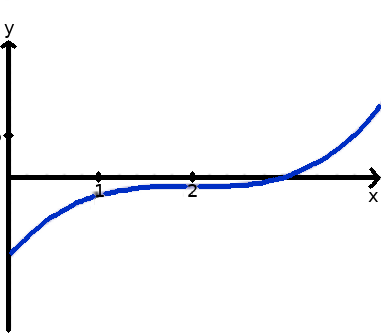
Der Funktionsgraph der nächsten Funktion zeigt die Funktion f(x) = (x - 2)³ - 1. Wie man auf den ersten Blick sieht ist diese nicht zum Ursprung punktsymmetrisch. Aber wie sieht es denn bei x = 2 aus? Dies sehen wir uns gleich rechnerisch weiter unten an.

Um zu prüfen, ob es eine Punktsymmetrie zu einem beliebigen Punkt gibt verwendet man die nächste Gleichung. Dazu haben wir einen beliebigen Punkt mit x und y-Koordinate und setzen diese in die Gleichung im Anschluss ein.

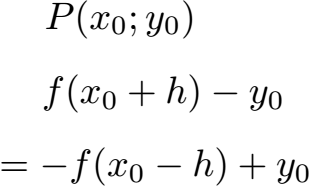
Anzeige:

Beispiel Punktsymmetrie zu Punkt rechnerisch

Sehen wir uns die Aufgabe zum Graphen weiter oben rechnerisch an.

Beispiel 1: Punktsymmetrie zu Punkt

Wir haben die nächste Funktion und einen Punkt. Ist die Funktion punktsymmetrisch zu diesem Punkt?

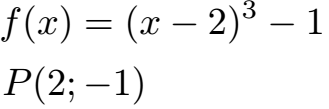
Lösung:

Wir lesen beim Punkt direkt x₀ = 2 und y₀ = -1 einfach ab. Im Anschluss müssen wir die Funktion testen. Wir nehmen dazu einfach die rechte Seite der Funktion mit (x - 2)³ - 1 und setzen für jedes Mal wo x vorkommt einfach x₀ + h dafür ein. Dadurch wird aus (x - 2) nun (x₀ + h - 2). Da x₀ = 2 ist können wir auch gleich 2 schreiben Die -1 bleibt stehen und im Anschluss brauchen wir noch - y₀. Da y₀ = -1 ist wird daraus - (-1).

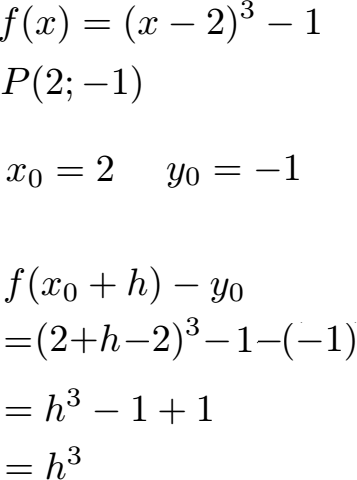
Im zweiten Schritt benötigen wir noch -f(x₀ - h) + y₀. Dies bedeutet zunächst das wir vor die ganze Funktion ein Minuszeichen schreiben, sprich alle Vorzeichen innerhalb der Klammer werden sich bei der Rechnung umdrehen. Ansonsten müssen wir wieder aus x nun x₀ - h machen. Aus (x - 2) wird dadurch (x₀ - h -2). Mit dem Wissen das x₀ = 2 ist vereinfacht sich die Klammer zu (2 - h₀ - 2). Dahinter fehlt noch die -1 aus der Ausgangsfunktion. Alles muss in Klammer gesetzt werden da die komplette Funktion mit dem Minuszeichen davor im Vorzeichen umgedreht werden soll. Fehlt uns noch + y₀ am Ende. Da y₀ = -1 ist kommt diese -1 noch am Ende hinzu.

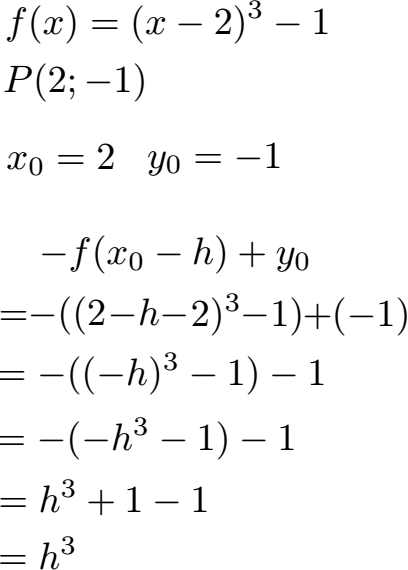
Nach der Vereinfachung sehen wir, dass wir in beiden Fällen h³ als Lösung erhalten. Dies bedeutet, dass die Funktion punktsymmetrisch zu unserem Punkt ist.

Aufgaben / Übungen Punktsymmetrie

Aufgabe 1:

Bevor wir rechnen bekommt ihr bei uns zunächst einige Verständnis- und Wissensfragen zur Punktsymmetrie.

• Es geht um Punktsymmetrie zum Ursprung. Welche Koordinaten hat dieser Ursprung?

• x = 0; y = 0
• x = 1; y = 1
• x = 10; y = 10
• x = -1; y = -1

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Punktsymmetrie

Fragen mit Antworten Punktsymmetrie zu einem Punkt