Berechnen Extremstellen, Extrempunkt und Extremwerte

Was Extrempunkte (Extremstellen und Extremwerte) sind und wie man sie berechnet, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, was Extrempunkte, Extremstellen und Extremwerte sind.
• Beispiele wie man diese Punkte berechnet.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zu Extrempunkten.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Für die Berechnung von Extrempunkten werden verschiedenen Regeln der Ableitung benötigt. Insbesondere die Potenzregel ist interessant, manchmal jedoch auch weitere Ableitungsregeln.

Extremstellen Erklärung

Nicht nur im realen Leben gibt es Hochpunkte und Tiefpunkte, sondern auch in der Mathematik. Diese bezeichnet man auch als Extrempunkte. In der nächsten Grafik seht ihr zwei Stellen mit einem Hochpunkt (auch Maximum genannt) und zwei Stellen mit einem Tiefpunkt (auch Minimum genannt).

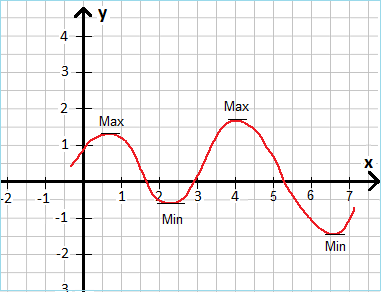
Manchmal ist von Extrempunkt, manchmal von Extremstelle und manchmal von Extremwert die Rede. Wo liegt der Unterschied?

• Der Extrempunkt ist ein Punkt mit x und y Angabe.
• Die Extremstelle ist nur der x-Wert vom Extrempunkt.
• Der Extremwert ist nur der y-Wert vom Extrempunkt.

Wie findet man Extrempunkt, Extremstelle oder Extremwert? Folgende Bedingungen sind wichtig:

• Die erste Ableitung Null setzen, f'(x) = 0.
  • Dies liefert mögliche Extremstellen (x_e genannt).
• Die zweite Ableitung an dieser Stelle x_e muss ungleich Null sein.
  • Ist f''(x_e) < 0 liegt ein Hochpunkt vor.
  • Ist f''(x_e) > 0 liegt ein Tiefpunkt vor.
  • Ist f''(x_e) = 0 steht Überprüfung für Sattelpunkt / Wendepunkt an.
• Die x_e-Werte werden in f(x) eingesetzt um y zu berechnen.
• Extrempunkt hat die Lage EP (x_e / f(x_e))

Im nächsten Abschnitt rechnen wir so ein Beispiel durch.

Anzeige:

Extrempunkt / Extremstelle berechnen

Sehen wir uns einmal an wie man Extrempunkte (Hochpunkt und Tiefpunkt) berechnet. Das Beispiel wird ausführlich vorgerechnet.

Beispiel 1: Extremstelle und Extrempunkt berechnen

Wo liegen die Extrempunkte der nächsten Funktion?

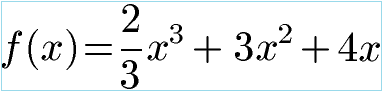
Lösung:

Wir benötigen von den Ableitungsregeln die Potenzregel um die erste Ableitung zu bilden.

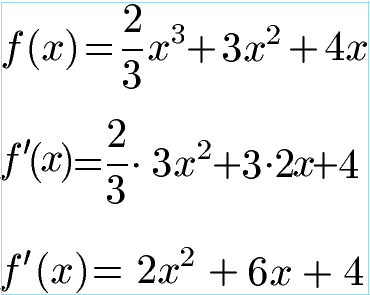
Im zweiten Schritt setzen diese Gleichung gleich Null, also f'(x) = 0. Wir erhalten eine quadratische Gleichung, welche wir mit der PQ-Formel lösen (Alternativ kann man auch die Mitternachtsformel verwenden). Dazu lesen wir p = 3 und q = 2 ab und setzen dies in die allgemeine Lösungsformel der PQ-Formel ein. Im Anschluss berechnen wir x₁ = -1 und x₂ = -2.

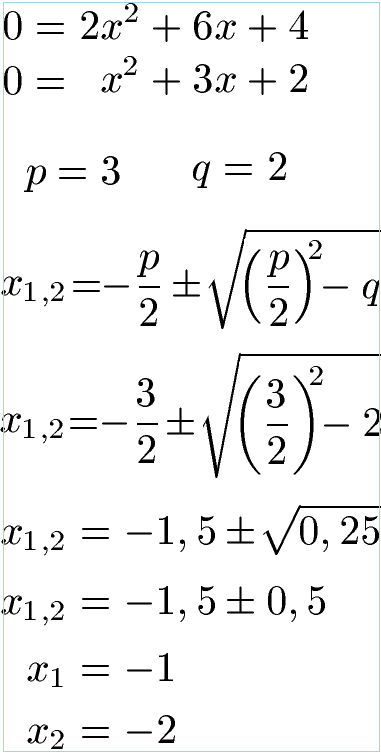
Bei x₁ = -1 und x₂ = -2 liegen mögliche Extrempunkte, welche wir nun näher untersuchen möchten. Mit der Potenzregel bilden wir noch die zweite Ableitung.

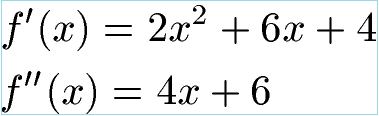
Um herauszufinden, ob es sich bei x₁ = -1 und x₂ = -2 um einen Extrempunkt handelt, setzen wir diese beiden x-Werte in f''(x) ein. Ist das Ergebnis größer als Null ist der Punkt ein Tiefpunkt. Ist das Ergebnis kleiner als Null liegt ein Hochpunkt vor.

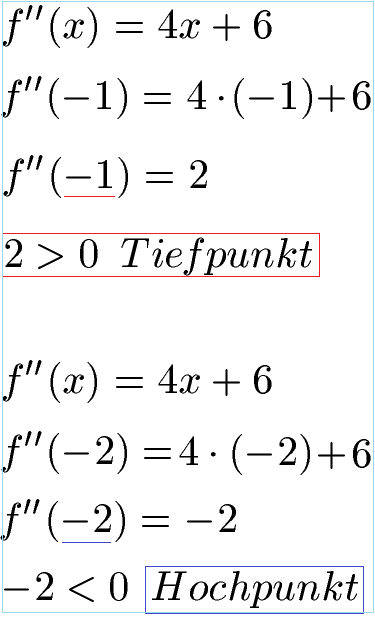
Die Rechnung zeigt, dass bei x₁ = -1 ein Tiefpunkt vorliegt und bei x₂ = -2 ein Hochpunkt. Wir kennen damit die x-Werte dieser Extrempunkte (also genauer gesagt kennen wir die Extremstelle). Jetzt berechnen wir noch deren y-Werte (also die Extremwerte). Dazu setzen wir x = -1 und x = -2 in die Ausgangsfunktion ein.

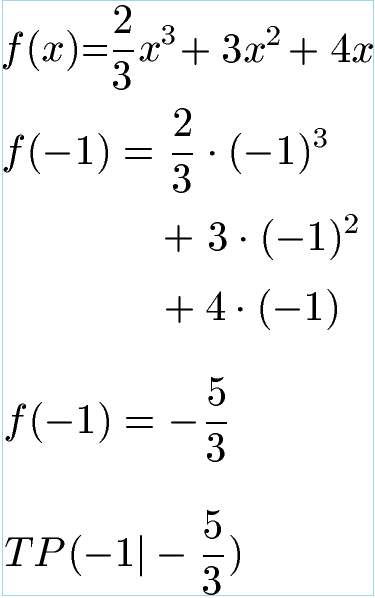
Wo liegen die Extrempunkte? Der Tiefpunkt liegt bei x = -1 und y = - 5 : 3. Den Hochpunkt berechnen wir gleich noch zu x = -2 und y = - 4 : 3.

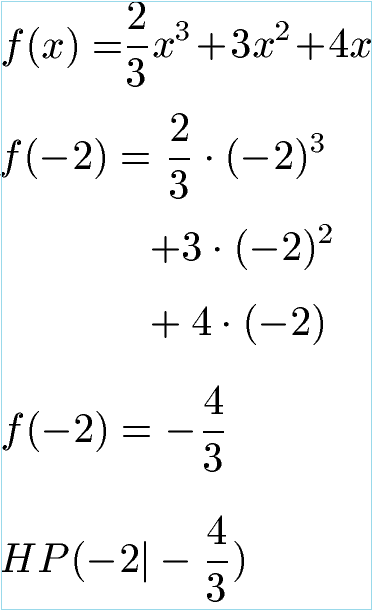
Aufgaben / Übungen Extrempunkte und Extremstellen

Aufgabe 1:

Wo liegt der Extrempunkt dieser Funktion?

• x = 1, y = 1
• x = 0, y = -1
• x = 0, y = 0
• x = -1, y = 0

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 2 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Extremstelle und Extremwert

Fragen mit Antworten Extrempunkt und Extremstelle