Verhalten im Unendlichen: Ganzrationale Funktion

Das Verhalten im Unendlichen für ganzrationale Funktionen sehen wir uns hier an. Dies sind die Themen:

• Eine Erklärung, was man unter dem Verhalten im Unendlichen versteht.
• Beispiele für die Berechnung dieser Grenzwerte.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zum Verhalten im Unendlichen.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Wir sehen uns hier das Verhalten im Unendlichen für ganzrationale Funktionen an. Wer dies etwas allgemeiner benötigt sieht in die Übersicht rein unter Verhalten im Unendlichen.

Ganzrationale Funktion Beispiel 1

Was versteht man unter der Untersuchung von ganzrationalen Funktionen im Unendlichen?

In vielen Fällen reicht ein geübter Blick auf die Funktion, um das Verhalten im Unendlichen zu ermitteln. Alternativ gibt es für einige Fälle Rechenregeln für die Bestimmung oder man kann sehr große bzw. sehr kleine Zahlen einsetzen.

Beispiel 1: Verhalten im Unendlichen

Nehmen wir die ganzrationale Funktion f(x) = 3x² -7x. Wie sieht deren Verhalten gegen plus unendlich und minus unendlich aus?

Lösung:

Bei ganzrationalen Zahlen sieht man sich den Ausdruck mit der höchsten Potenz an. In unserem Fall 3x². Denn der Ausdruck mit der höchsten Potenz steigt am schnellsten oder fällt am schnellsten wenn sehr große oder sehr kleine Zahlen eingesetzt werden. Dies bedeutet, dass wenn man für x immer größeren Zahlen einsetzt (10, 100, 1000 etc.) das Ergebnis immer größer wird. Setzen wir immer kleinere Zahlen ein (-10, -100, -1000, etc.) passiert dies auch, denn durch hoch 2 (quadrieren) fliegt das Minuszeichen raus. Unter dem Strich kommt plus unendlich in beiden Fällen raus.

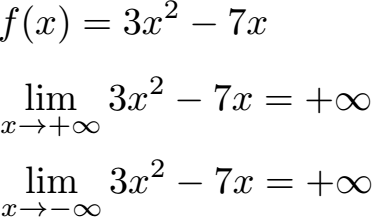
Anzeige:

Ganzrationale Funktion Beispiele

Wer bei Funktionen Probleme hat zu sehen, wie das Verhalten im Unendlichen ist, der kann einfach einmal Zahlen einsetzen. Nehmen wir dazu noch einmal unser Beispiel von oben.

Beispiel 1 mit Zahlen:

Wir nehmen erneut f(x) = 3x² - 7x. In die Funktion setzen wir x = 100 ein und x = 1000. Wie man an den Ergebnissen von 29300 und 2993000 sehen kann, wächst das Ergebnis mit steigendem x stark an. Dies würde auch passieren, wenn man -100 oder -1000 einsetzen würde.

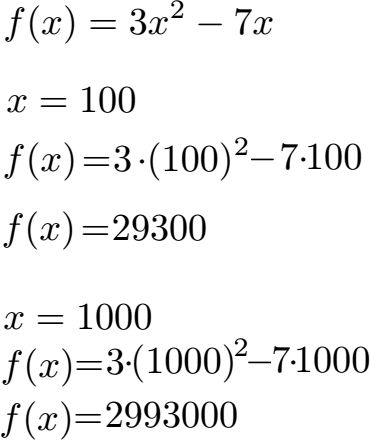
Beispiel 2 ganzrationale Funktion:

Wie sieht das Verhalten der Funktion f(x) = -2x³ +2x² gegen plus unendlich und minus unendlich aus?

Lösung:

Wie auch bei anderen ganzrationalen Funktionen werfen wir einen Blick auf die höchste Potenz, in diesem Fall -2x³. Setzen wir für x große Zahlen ein wächst x³ stark an. Das Minuszeichen am Anfang sorgt jedoch dafür das alle Zahlen negativ werden, daher geht das Ergebnis gegen minus unendlich. Setzen wir hingegen negative Zahlen ein dreht sich das Verhalten um. Beispiel -2 · (-10)(-10)(-10) = -2 · (-1000) = + 2000. Das heißt das Ergebnis wächst positiv ins Unendliche.

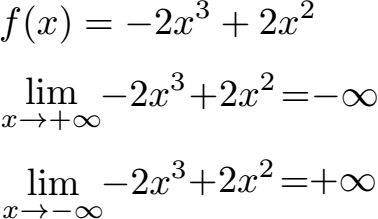
Aufgaben / Übungen Verhalten im Unendlichen

Aufgabe 1:

• Wie sieht das Verhalten der folgenden Funktion gegen plus unendlich aus?

• 0
• kein Grenzwert
• plus unendlich
• minus unendlich

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 12 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Verhalten im Unendlichen

Fragen mit Antworten: Verhalten im Unendlichen für ganzrationale Funktionen