Achsensymmetrie / Spiegelsymmetrie
Geschrieben von: Dennis RudolphMontag, 16. Dezember 2019 um 10:28 Uhr
Mit der Achsensymmetrie bzw. Spiegelsymmetrie befassen wir uns hier. Dies sehen wir uns an:
- Eine Erklärung, was man unter Achsensymmetrie (Spiegelsymmetrie) versteht.
- Beispiele wie man diese Art der Symmetrie berechnet.
- Aufgaben / Übungen um das Thema selbst zu üben.
- Ein Video zur Symmetrie von Funktionen.
- Ein Frage- und Antwortbereich zu diesem Thema.
Tipp: Es ist hilfreich wenn ihr bereits wisst wie man eine Funktion zeichnet.
Erklärung Achsensymmetrie
Mit der Symmetrie von Funktionen und Körpern beschäftigt man sich bereits ab der Grundschule. In der Oberstufe geht es darum die Punktsymmetrie und die Achsensymmetrie (Spiegelsymmetrie) auch zu berechnen. Wichtig: Ist von Achsensymmetrie die Rede ist meistens damit die Symmetrie zur y-Achse gemeint.
Die nächste Grafik zeigt die Funktion y = x2. Wie man sehen kann ist diese Funktion spiegelsymmetrisch zur y-Achse. So kann man jeden Punkt von links nach rechts oder umgekehrt spiegeln. Seht es euch an:
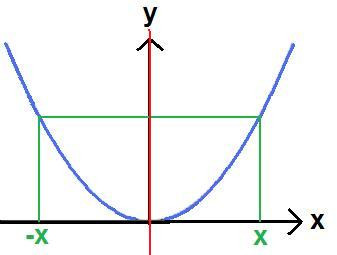
Wir halten fest:
Eine gerade Funktion ist spiegelsymmetrisch zur y-Achse. Jeder Punkt kann an der y-Achse gespiegelt werden und landet auf der anderen Seite der y-Achse wieder auf dem Funktionsgraphen. Die Gleichung bzw. Formel zur Überprüfung lautet:
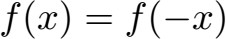
Anzeige:
Anzeigen:
Beispiele Spiegelsymmetrie
Sehen wir uns an wie man rechnerisch die Spiegelsymmetrie (Achsensymmetrie) berechnet.
Beispiel 1: Achsensymmetrie testen
Ist die folgende Funktion achsensymmetrisch zur y-Achse?
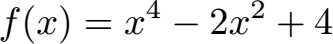
Lösung:
Wir kennen bereits f(x). Benötigen tun wir zusätzlich f(-x). Daher ersetzen wir in unserer Funktion jedes x durch ein -x. Beachtet dabei das Setzen von Klammern, denn wenn hoch 2, hoch 3, hoch 4 etc. berechnet werden soll muss das Minuszeichen ebenfalls genutzt werden. Im Anschluss vereinfachen wir die Gleichung und sehen das f(x) = f(-x) ist. Daher ist die Funktion achsensymmetrisch zur y-Achse.
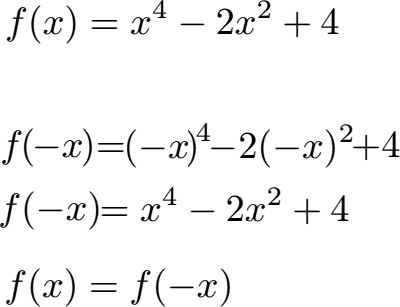
Beispiel 2: Achsensymmetrie testen
Ist die nächste Funktion achsensymmetrisch zur y-Achse?
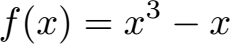
Lösung:
Wir ersetzen jedes x durch -x. Beim Ersetzen müssen Klammern gesetzt werden. Im Anschluss vereinfachen wir und sehen, dass f(x) und f(-x) verschieden sind. Wir haben damit keine Achsensymmetrie zur y-Achse.
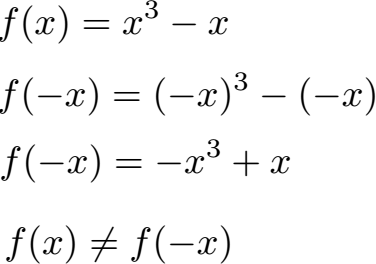
Aufgaben / Übungen Achsensymmetrie
Anzeigen:Video Symmetrie
Erklärungen und Aufgaben
Dies sehen wir uns im nächsten Video zur Symmetrie an:
- Erklärung Achsensymmetrie
- Erklärung Spiegelsymmetrie
- Erklärung Punktsymmetrie
- Erklärung Punktsymmetrie berechnen
Zu den Arten der Symmetrie gibt es
- Erläuterungen und
- Übungen werden vorgerechnet.
Nächstes Video »
Fragen mit Antworten zur Achsensymmetrie
In diesem Abschnitt sehen wir uns typische Fragen mit Antworten zur Achsensymmetrie (Spiegelsymmetrie) zur y-Achse an.
F: Wann wird das Thema Achsensymmetrie in der Schule behandelt?
Die Grundlagen der Achsensymmetrie in der Mathematik werden bereits in in der 3. Klasse und 4. Klasse besprochen. Wir sehen uns hier jedoch typische Untersuchungen zur Achsensymmetrie an, wie diese in der Oberstufe und im Abitur auf dem Schulplan stehen. Dabei werden die Gebiete und Begriffe Punktsymmetrie, Spiegelsymmetrie und Achsensymmetrie geklärt.
F: Welche Ableitungsregeln und Ableitungsthemen sollte ich kennen?
A: Die folgenden Themen werden in der Schule zu Ableitungen behandelt.
- Differentialrechnung Übersicht
- Ableitung: Grundlagen und Definition
- Ableitung Tabelle / Ableitungstabelle
- Ableitungsregeln
- Kurvendiskussion
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
